
The solar spectral distribution in terms of the solar energy outside the Earth's atmosphere per unit area and wavelength range, as expressed in energy units, is given in the following plot. Also shown is the relative visibility factor K for normal brightness (cone vision at fovea, not rod nighttime vision).
The quantity plotted, energy units, is the wavelength times the energy per unit wavelength and thus accurately represents the amount of energy at any wavelength. The energy per unit wavelength and the energy per unit frequency peak at significantly different wavelengths due the reciprocal relation between frequency and wavelength. Using energy units avoids this problem, since (wavelength * flux per unit wavelength) = (frequency * flux per unit frequency). The archaic unit used for wavelength is the micron, 10-6 m, since we astronomers are pretty fixed in our ways. It is abbreviated mu on the plot since the greek symbol mu was not available to form the abbreviation micro-meter.

The integrated solar energy is given in the following plot, again along with the relative visibility factor. The total integral is 1.36 kW / m^2 outside the Earth's atmosphere.
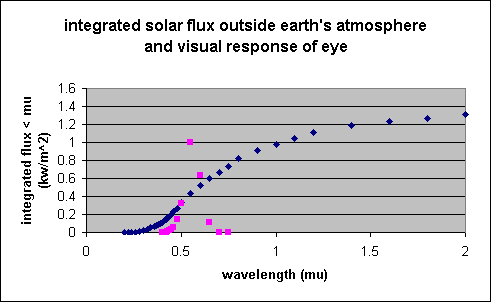
It is of some interest what fraction of the solar energy is seen by the eye. However, I'm not 100% sure what the relative visibility factor means, so I'll calculate it in two ways. First, if one assumes that the eye picks up all solar radiation between the points at which the eye response is 0.01, the "solar constant" in that way is roughly 0.6 KW / m^2. Second, if one assumes that the relative visibility factor is actually a quantum efficiency, the integration of the solar constant multiplied by the relative visibility factor is roughly 0.2 KW / m^2, a very different number.
If you know the correct interpretation of the relative visibility factor, please let me know.
Source: Allen, C.W. Astrophysical Quantities, 3rd edition, 1973, p. 109, 172.
The relationship between color and wavelength is:
| Color | Representative Wavelength (microns) | Wavelength Range (microns) |
|---|---|---|
| Violet | 0.41 | 0.400-0.424 |
| Indigo | 0.44-0.45 | ?? |
| Blue | 0.47 | 0.4240-0.4912 |
| Green | 0.52 | 0.4912-0.5750 |
| Yellow | 0.58 | 0.575-0.585 |
| Orange | 0.60 | 0.585-0.647 |
| Red | 0.65 | 0.647-0.700 |
Yes, I know that there seems to be a ridiculous number of figures in the above table. But I'm just reading the table, and don't know how to round appropriately or whether there is some actual justification for the number of places. If you know, please email me!
Source: CRC Handbook of Chemistry and Physics, 1966, p. E-126; Abell, Exploration of the Universe,1969, p. 204.
There is no sharp cutoff to human vision, so violet and red colors can extend to shorter and longer wavelengths, respectively. For example, the human eye detects only 1% of light at 0.69 microns, and 0.01% at 0.75 microns, and so effectively cannot see wavelengths longer than about 0.75 microns unless the light source is extremely bright. (Source: Allen, 1973, as quoted above.)
Go To:
Copyright © 1998-1999 by Tom Chester.
Permission is freely granted to reproduce any or all of this page as long as credit is given to me at this source:
http://la.znet.com/~schester/facts/solar_energy.html
Comments and feedback: Tom Chester
Last update: 29 September 1999.